はじめに

SPIで出題される「推論」は、非言語の中でも最も優先して対策すべき分野です。
後半でも述べますが、「推論が連続して出題される」=「高得点をマークしている」ことの裏付けです。
つまり、極論を言えば推論さえ極めればSPI非言語は敵なしです。
本サイトでは、SPI・玉手箱など各種適性検査の対策問題を更新しています。
本日はSPI「推論」分野。全3問です。
問題1
問題
目標回答時間:30秒
P、Q、R、S、Tの5人で徒競走をした。
5人の順位について、次のことが分かっている。
- Rの順位はSよりも上である
- Tの順位はRよりも上だが、1着では無かった。
- Qの順位はPよりも上である。
- 同着の順位の者はいなかった。
次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- Qは1着である。
- Sは5着である。
- 2着はPまたはTである。
解答
解答を表示
非常にオーソドックスな推論問題です。
推論問題は、
基本的に全パターンを愚直に列挙するのが回答への近道です。
以降、左に位置するほうが早くゴールしたことを示す不等式で表すとして、与えられた条件を整理すると、
ということが分かり、①と②からT>R>Sの順番でゴールした事がわかります。
Tは1着ではなく、Tより後に少なくとも2人はゴールしたことを考えると、Tは2位または3位だと確定します。
ここで、③を踏まえた上で全パターンを列挙しましょう。
(1)Tが2位の場合:Q>T>P>R>S、Q>T>R>P>S、Q>T>R>S>Pの3通り
(2)Tが3位の場合:Q>P>T>R>Sの1通り
以上4通りが考えられるすべての順位です。
したがって、3つの推論のうち必ず正しいのはアおよびウであることが分かります。
★与えられた条件を整理した段階で、あれこれ考えるより考えられるパターンをすべて列挙しましょう。
問題2
問題
目標回答時間:40秒
A、B、C、D、Eの5人がカウンターに向かって一列に並んだ6つの椅子のいずれかに座っている。
各自の座り方について、次のことが分かっている。
- Eの隣に空席があった
- BとCの席は隣り合っていた
- 両端の席は空席ではなかった
AとDが隣り合っていたとき、下のU、V、W、X、Y、Zのうち、Eが座った可能性がある席をすべて選びなさい。

解答
解答を表示
いわゆるチェックボックス型推論問題であり、対策優先度がかなり高い問題。
とはいえ、しっかり方針を立てて考えられれば直ぐに解くことができます。
まずは与えられた3つの条件を整理します。以下、空席を○として表します。
- Eの隣に空席があった→E○もしくは○E
- BとCは隣り合っていた→BCもしくはCB
- 両端は空席でなかった→V、W、X、Yのいずれか1つに○が来る
- AとDが隣り合っていた→ADもしくはDA
(1)Vが空席の場合
UまたはWにEが入る余地がある。
UにEが来ると、WX・YZにそれぞれADまたはBCペアを入れることができるので適する。→U
WにEが来ると、隣り合うAD・BCペアが入れないので不適。
(2)Wが空席の場合
VまたはXにEが入る余地がある。
VにEが来ると、隣り合うAD・BCペアが入れないので不適。
XにEが来ると、UV・YZにそれぞれADまたはBCペアを入れることができるので適する。→X
(3)Xが空席の場合
WもしくはYにEが入る余地がある。
WにEが来ると、UV・YZにそれぞれADまたはBCペアを入れることができるので適する。→W
YにEが来ると、隣り合うAD・BCペアが入れないので不適。
(4)Yが空席の場合
XもしくはZにEが入る余地がある。
XにEが来ると隣り合うAD・BCペアが入れないので不適。
ZにEが来るとUV・WXにそれぞれ隣り合うAD・BCペアを入れることが出来るので適する。→Z
したがって、Eが入る余地がある場所はU、W、X、Zの4箇所である。
★偶数ペアがAD・BCの2つあるので、Eを入れた時点で飛び地ができると不適だと分かります。
問題3
問題
目標回答時間:1分30秒
P、Q、R、S、Tの5人が、昨年と今年のテストの点数を比較したところ、次の4つのことがわかった。
- Rの点数は2年ともSより高かった。
- Tの今年の順位は、昨年から3つ下がった。
- 2年とも、Qの点数はPの次に高かった。
- 昨年と今年で同じ順位の人はいなかった。
最も少ない情報で5人の昨年と今年のテストの点数の順位を確定させるためには、次のア、イ、ウのうちどれが加わればよいか。
- 今年のPの順位は1位である。
- 昨年のRの点数はTよりも高かった。
- Sの今年の順位は、昨年の順位よりも高かった。
解答
解答を表示
めちゃくちゃ面倒くさい問題。まずは条件を整理しましょう。
- 条件1より、2年ともR>S…①
- 条件2より、Tの順位は昨年1位今年4位または昨年2位今年5位の2通り…②
- 条件3より、2年ともP>Qであり、PとQは連続している…③
- 条件4より、2年連続で同じ順位を取ることはできない…④
ここで②を用いて場合分けする。
(1)昨年のTの順位が1位だった場合
昨年の順位は、①および③より2位はPまたはRだから、(i)T>P>Q>R>S、(ii)T>R>S>P>Q、(iii)T>R>P>Q>Sの3パターン
今年の順位は、①および③より1位はPまたはR、かつTの順位は4位だから、(iv)P>Q>R>T>S、(v)R>P>Q>T>Sの2パターン
ここで④より、今年の2パターン両方において「S5位」が一致しており、(i)および(iii)が条件に反し不適だと分かる。
したがって、昨年は(ii)で確定し、今年は(iv)または(v)である。
(2)昨年のTの順位が2位だった場合
昨年の順位は、①および③より1位に入りうる人物がRのみであることが分かる。(Pが入るとするとQが2位になりダブるから)
したがって、昨年の順位は(vi)R>T>S>P>Q(vii)R>T>P>Q>Sの2パターン
今年の順位は、(viii)P>Q>R>S>T (ix)R>P>Q>S>T(x)R>S>P>Q>Tの3パターン
ここで④より、昨年の2パターン両方において「R1位」が一致しており、(ix)および(x)が条件に反し不適だとわかる。
したがって、昨年は(vi)または(vii)であり、今年は(viii)で確定する。
以上、(1)(2)より考えられるパターンは、
- 昨年:(ii)T>R>S>P>Q今年:(iv)P>Q>R>T>S
- 昨年:(ii)T>R>S>P>Q今年:(v)R>P>Q>T>S
- 昨年:(vi)R>T>S>P>Q今年:(viii)P>Q>R>S>T
- 昨年:(vii)R>T>P>Q>S今年:(viii)P>Q>R>S>T
の4パターンであることが分かる。ここでア、イ、ウを考える。
- 今年のPの順位が1位→(a)、(c)、(d)の3択になり、1つに絞れない。
- 昨年度、R>T→(c)、(d)の2択になり、1つに絞れない。
- Sの順位が今年>昨年→(d)の1択になり、これが正解。
SPI推論について
 SPI非言語分野のなかでも、推論は特に優先して対策すべき分野です。
SPI非言語分野のなかでも、推論は特に優先して対策すべき分野です。
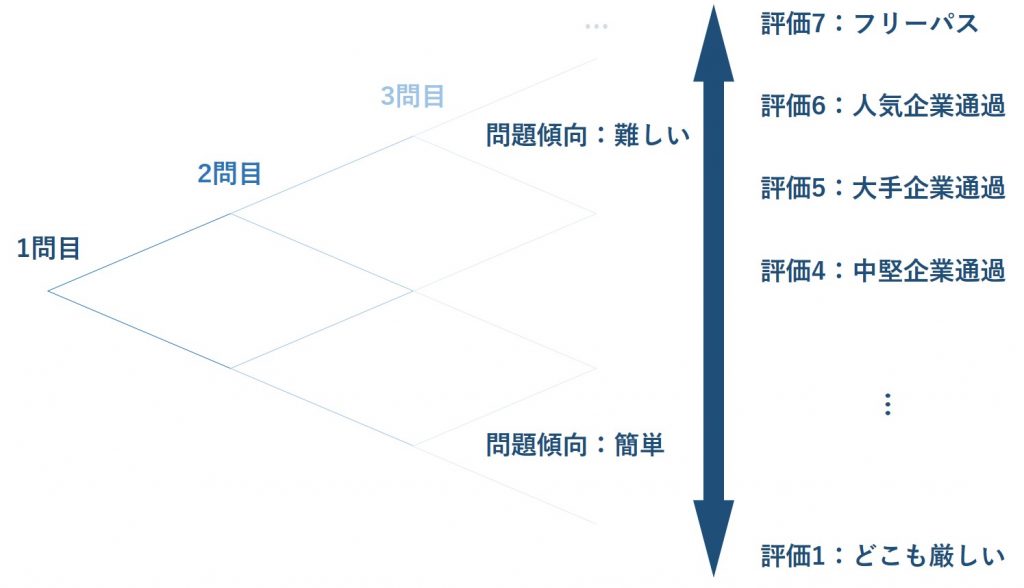
SPIは上図のような仕組みになっており、正答を重ねるごとに難しい問題が出題されるようになっています。
これを繰り返すことで、帰納的に学生の能力が7段階で評価されます。
そして、この傾向でいう「難しい問題」に推論は分類されるため、大手企業の筆記試験に通過しようと思うと、必ず避けては通れません。
むしろ、「簡単な問題」に分類される確率や速度算などの計算問題は、一定レベル以上の大学生ならばそつなくこなしますので、差をつけられません。
受験企業のレベルに合わせて、優先して対策すべき問題レベルを設定することをオススメします。
もっとSPIの問題を解く
基本的に、SPIは解法暗記によってコンスタントに高得点を獲得することが可能です。
そして、そのためにはたくさんの問題に触れることが一番です。
問題集などを購入するのも良いですが、当サイトでは完全無料でSPIや玉手箱などの対策問題を公開しています。
就職活動は、交通費や衣服費など出費がかさむイベントでもあります。
節約できるところは節約して、賢く就職活動を攻略しましょう!
新しい問題を追加した際にはTwitter(@shu_strategy)でお知らせします!
適性検査対策問題一覧


 SPI非言語分野のなかでも、推論は特に優先して対策すべき分野です。
SPI非言語分野のなかでも、推論は特に優先して対策すべき分野です。














